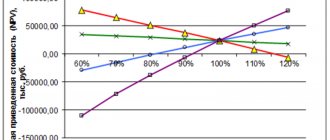
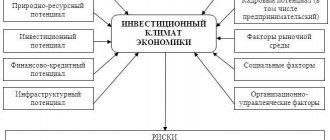
Приведем пример формирования инвестиционного портфеля по модели Г. Марковица с помощью программы Excel, разберем достоинства и недостатки данной модели в современной экономике и пути их решения.
Инвестиционный портфель – это совокупность различных финансовых инструментов, удовлетворяющих цели инвестора и, как правило, заключается в создании таких комбинаций активов, которые бы обеспечили максимальную доходность при минимальном уровне риска.
Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс
Курсы закрытия
В расчетах будем использовать дневные курсы закрытия closeData = data.Close closeData
Графики курсов
import matplotlib.pyplot as plt for name in closeData.columns: closeData[name].plot() plt.grid() plt.title(name) plt.show()
Стратегии управления инвестициями
Существуют две основные стратегии: активная и пассивная
Активное управление предусматривает то, что инвестор постоянно должен держать “руку на пульсе”: изучать новости, аналитику, мнения специалистов и другую информацию и совершать ребалансировку своего портфеля в соответствии с нею.
Пассивная тактика предполагает следование принципу “купил и забыл”. Инвестору не нужно постоянно следить за рынком. В основном он инвестирует на продолжительный срок в надежные инструменты, что не требует постоянной корректировки. Это проще, чем придерживаться активной тактике.
Графики относительных изменений курсов
for name in dCloseData.columns: dCloseData[name].plot() plt.title(name) plt.grid() plt.show()
Построение портфеля Г. Марковица в Excel для российского фондового рынка
В данной статье при помощи средств Ecxel создается оптимальный по Г. Марковицу портфель для акций российского фондового рынка.
{module 297}
Портфель – это совокупность финансовых активов, объединенных вместе для реализации целей инвестора, для максимизации прибыли и минимизации убытков.В модели Марковица допустимыми являются только стандартные портфели, портфели без коротких позиций(без продаж), то есть портфель состоящий только из купленных акций. Отсюда первое ограничение, которое накладывается на портфель, это положительные доли всех ценных бумаг (хi).
(1)
Второе ограничение состоит в том, что сумма всех долей ценных бумаг должна составлять 1, это правило нормировки долей. Формула 2 показывает это ограничение.
(2)
Так же доходность портфеля будет выглядеть как сумма доходностей отдельных акций с выбранными весовыми коэффициентами. Так как каждый инвестор пытается максимизировать получаемую доходность, то необходимо будет максимизировать эту целевую функцию. В итоге это будет выглядеть в виде формулы 3.
(3)
Помимо доходности инвестору необходимо так же учесть и риск, связанный с той или иной акцией. Риск по Г. Марковицу выражается в виде среднеквадратического отклонения δi каждой акции. Значение δр – это уровень приемлемого риска для инвестора. Помимо учета средне квадратического отклонения отдельных акций необходимо учесть корреляцию между доходностями акций – rij . Корреляция в нашем случае для модели Марковица равняется нулю. В итоге риск всего портфеля представлен формулой 4.
(4)
Экономико-математическая модель задачи формирования оптимального портфеля акций максимальной эффективности при которой риск портфеля не превышает заданного значения δр , и при учете всех ограничений на портфель, примет следующий вид (5):
(5)
{module 297}
Обратная задача оптимизации портфеля сводится к выбору такой структуры портфеля, доходность которого выше либо равна заданному значению mp, а риск минимален. Экономико-математическая модель задачи в этом случае примет вид(6):
(6)
Пример составления портфеля Марковица для российского фондового рынка
Для примера возьмем акции 4-х российских компаний Газпром (GAZP), Дальсвязь(DLSV), Сургутнефтегаз (SNGS) и Роснефть (ROSN). Построим на основе котировок оптимальный портфель. Для нахождения оптимального портфеля по Марковицу воспользуемся средствами Excel и компонентой Solver(Поиск решений). Для начала рассчитаем дневную доходность по каждой акции за один год с 20.05.2009 по 20.05.2010. Формула расчета дневной доходности (mj) представлена (7): ;
(7)
Где: Рj – цена акции на конец текущего дня; Рj-1 – цена акции за предыдущий день. В итоге должна получится следующая таблица дневных доходностей каждой из акций:
Что бы рассчитать доходность для каждой акции необходимо найти среднюю доходность акции за выбранный период, в данном случае 1 год.
(8)
Посчитав, среднедневная доходность за весь период составила для GAZP = -0,02%, DLSV =0,28%, SNGS =0,05% и ROSN= 0,08%. Так как средняя доходность Газпрома отрицательная то эта акция не будет включена в портфель. Помимо доходности необходимо рассчитать риск этих акций, для этого рассчитаем среднеквадратическое отклонение дневных доходностей акций по формуле (9).
(9)
Для Дальсвязи (DLSV) δ1 =1,73% , Сургут нефтегаза (SNGS) δ2 = 1,98% и Роснефти (ROSN) δ3 = 2,05%. Составим уравнение для нахождения оптимального портфеля. Так же зададим допустимый максимальный уровень риска в 0,15%.
(10)
Полученные данные занесем в таблицу для расчетов долей (xi) каждой акции в портфеле. Осталось решить полученное уравнение и рассчитать доли каждой акции, для этого воспользуемся встроенным в пакет Excel надстройки «Поиск решений».
После запуска надстройки «Поиск решений» установим целевую функцию, это доходность всего портфеля. После этого поставим флажок на максимизации значения этой целевой функции. Ячейки для изменения будут соответствовать доли акций, которые необходимо найти. Так же необходимо наложить ограничения на то что бы сумма всех долей была равна 1, и что бы каждая доля была не отрицательна и общий риск портфеля был бы меньше 0,15%. В ячейке с общим риском (D7) прописывается следующая формула: =КОРЕНЬ(0,0301*D2*D2+0,0393*D3*D3+0,0421*D4*D4) Целевая функция в ячейке (F3) равняется: =D2*B2+D3*B3+D4*B4 В ячейке (D6) прописывается ограничение для портфеля: =СУММ(D2:D4) После проделанной работы определятся доли в инвестиционном портфеле для каждой акции.
Расчет оптимального портфеля по Г. Марковицу представлен на рисунке ниже. Оптимальный портфель будет состоять из 85,38% акций Дальсвязи (DLSV), 3,66% акций Сургутнефтегаза (SNGS) и 10,96% акций Роснефти (ROSN). Доходность всего портфеля будет составлять 0,24% при общем установленном заранее риске портфеля в 0,15%.
{module 297}
Автор: Жданов Иван www.beintrend.ru
Облако портфелей
Сгенерируем множество портфелей и выведем результат на график риск-доходность. Найдем параметры оптимального портфеля по минимальному риску и по максимальному коэффициенту Шарпа. Сравним с данными усредненного портфеля. risk = np.zeros(N) doh = np.zeros(N) portf = np.zeros((N,cnt)) for n in range(N): r = randPortf() portf[n,:] = r risk[n] = riskPortf(r) doh[n] = dohPortf(r) plt.figure(figsize=(10,8)) plt.scatter(risk*100,doh*100,c=’y’,marker=’.’) plt.xlabel(‘риск, %’) plt.ylabel(‘доходность, %’) plt.title(«Облако портфелей») min_risk = np.argmin(risk) plt.scatter([(risk[min_risk])*100],[(doh[min_risk])*100],c=’r’,marker=’*’,label=’минимальный риск’) maxSharpKoef = np.argmax(doh/risk) plt.scatter([risk[maxSharpKoef]*100],[doh[maxSharpKoef]*100],c=’g’,marker=’o’,label=’максимальный коэф-т Шарпа’) r_mean = np.ones(cnt)/cnt risk_mean = riskPortf(r_mean) doh_mean = dohPortf(r_mean) plt.scatter([risk_mean*100],[doh_mean*100],c=’b’,marker=’x’,label=’усредненный портфель’) plt.legend() plt.show()
Выведем данные найденных портфелей.
import pandas as pd print(‘———- Минимальный риск ———-‘) print() print(«риск = %1.2f%%» % (float(risk[min_risk])*100.)) print(«доходность = %1.2f%%» % (float(doh[min_risk])*100.)) print() print(pd.DataFrame([portf[min_risk]*100],columns=dCloseData.columns,index=[‘доли, %’]).T) print() print(‘———- Максимальный коэффициент Шарпа ———-‘) print() print(«риск = %1.2f%%» % (float(risk[maxSharpKoef])*100.)) print(«доходность = %1.2f%%» % (float(doh[maxSharpKoef])*100.)) print() print(pd.DataFrame([portf[maxSharpKoef]*100],columns=dCloseData.columns,index=[‘доли, %’]).T) print() print(‘———- Средний портфель ———-‘) print() print(«риск = %1.2f%%» % (float(risk_mean)*100.)) print(«доходность = %1.2f%%» % (float(doh_mean)*100.)) print() print(pd.DataFrame([r_mean*100],columns=dCloseData.columns,index=[‘доли, %’]).T) print() ———- Минимальный риск ———- риск = 1.80% доходность = 0.59% доли, % AAPL 53.890706 AMD 12.793389 BAC 4.117541 F 16.547201 GE 10.945462 PLUG 1.705701 ———- Максимальный коэффициент Шарпа ———- риск = 2.17% доходность = 0.88% доли, % AAPL 59.257114 AMD 8.317192 BAC 2.049882 F 8.689935 GE 4.772159 PLUG 16.913719 ———- Средний портфель ———- риск = 2.33% доходность = 0.68% доли, % AAPL 16.666667 AMD 16.666667 BAC 16.666667 F 16.666667 GE 16.666667 PLUG 16.666667
Определение меры риска
Итак, мы приняли за эффективность избранной нами ценной бумаги случайную (с точки зрения теории вероятности) величину X.
Тогда мерой риска этой величины будет ее ДИСПЕРСИЯ
. На языке формул значение меры риска (дисперсии) можно записать так:
Z =
U {(X –m)2}
.
Величина Z всегда больше либо равна нулю.
Чем меньше значение Z, тем ниже степень риска, присущая соответствующей ценной бумаге (или – тут большой разницы нет — портфелю ценных бумаг).
Ежели Z = 0, мы имеем дело с безрисковым портфелем.
Выводы
Повторили классический метод расчета долей инвестиционного портфеля. Получили вполне конкретные результаты.
Оптимизация портфеля по методу Марковица предполагает сохранение параметров в будущем (корреляций между отдельными инструментами и уровня их доходности). Но это не гарантировано. В следующих работах предстоит это проверить.
Понятно, что положительного результата от обозначенной выше проверки ожидать не стоит. Но тогда можно поискать как доработать метод Марковица для получения более гарантированного дохода в будущем. Вот тема для еще одного исследования.
Портфельная теория Марковица — что это?
Книга на русском языке «Портфельная теория Марковица» вышла в 2013 году и направлена на грамотный подход в инвестировании. Основной подход в том, чтобы среди всего разнообразия инструментов найти те, которые отвечают высокой доходности при незначительном риске. Сама теория известна и ею активно пользуются практически 60 лет, хотя и с небольшими доработками.
Интересный момент, что ключевые постулаты теории были сформулированы в 50-х годах, и за это время не только не потеряли популярности, но стали более актуальными. Говоря глобально: теория портфельного вложения и предварительного анализа рынка Марковица стимулирует владеть активами, а не играть на биржевых рынках. Иногда портфельная теория отождествляется не только с Марковицем, но и Шарпом — американскими учеными-экономистами. У. Шарп предложил свою рыночную, менее трудоемкую индексную теорию оценки активов позже, чем Марковиц в 60-х годах, но Нобелевскую премию получил также в 1990 году. Помимо того, что его теория менее оборонительная для инвестора, она рассматривает доходность каждой ценной бумаги по отношению ко всему рынку, а его коллега предлагает сравнивать их между собой.