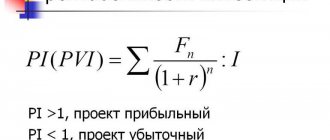olegas Дек 18, 2021 / 269 Views
Один известный фьючерсный трейдер сказал, что при одинаковом уровне дохода по итогам года у нескольких трейдеров, коэффициент Шарпа показывает, кто из них добился его за счёт своего мастерства (преимущества на рынке), а кто за счёт принятия слишком высоких рисков. Очевидно, что ставку следует делать на первых, на тех, кто добивается результатов, сохраняя при этом приемлемый уровень риска, исключительно за счёт своего трейдерского мастерства. Так как понятно, что высокие риски, рано или поздно, приводят к значительным убыткам (зачастую к полному сливу депозита).
Если в двух словах, то коэффициент Шарпа показывает какую прибыль получает трейдер на единицу риска
Для начала совсем немного истории. Впервые данный коэффициент увидел свет в 1966 году благодаря стараниям будущего нобелевского лауреата Уильяма Шарпа (свою Нобелевскую премию он получит через 44 года за разработку модели для оценки капитальных активов CAPM).
Формула расчета коэффициента Шарпа
где:
rp – средняя доходность паевого инвестиционного фонда (инвестиционного портфеля);
rf – средняя доходность безрискового актива;
σp – стандартное отклонение доходностей активов паевого инвестиционного фонда (риск инвестиционного портфеля).
Рассмотрим более подробно, как рассчитать каждый из показателей формулы.
| ★ Excel таблица для формирования инвестиционного портфеля ценных бумаг (рассчитай портфель за 1 минуту) + оценка риска и доходности |
| ★ Программа InvestRatio – расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса |
Стандартное отклонение
Коэффициент Шарпа оценивает эффективность инвестиции с точки зрения дисперсии доходов. Так как мы уже подсчитали избыточную доходность (доходность за вычетом безрисковой ставки), осталось поделить это значение на стандартное отклонение доходности актива. То есть, посчитать отношение доходности к риску.
Хотя сегодня это уже и не требуется, все же стандартное отклонение несложно рассчитать вручную. Допустим, вы собрали небольшую статистику доходности сделок: 3%, 4%, 5%, 2%, 1%. На первом этапе мы вычитаем из этой последовательности среднее и получаем такой ряд: 0%, 1%, 2%, -1%, -2%.
Далее, возводим значения в квадрат, получаем арифметическое среднее и выводим корень от результата – sqrt((0.00% + 0.01% + 0.04% + 0.01% + 0.04%) / 5) = 1.41%.
Для сравнения, возьмем немного другую выбрку: 2%, 8%, 5%, 4%, 6%. Очевидно, что доходность такой системы в рамках рассматриваемого периода больше, но мы также наблюдаем гораздо большую волатильность доходности, 2% против 1.41% у предыдущего примера. Соответственно, первая стратегия является менее рискованной.
Расчет доходности безрискового актива
Для оценки избыточной доходности, которую получил инвестор необходимо рассчитать минимальную возможную доходность, которую он мог бы получить при вложении в абсолютно надежные активы. Именно избыточная доходность отражает качество управления и эффективность принимаемых решений менеджером паевого инвестиционного фонда.
Существуют несколько способов оценки доходности безрискового актива:
- Доходность банковского вклада наиболее крупных и надежных банков РФ. К таким банкам можно отнести Сбербанк, Альфа-банк, ВТБ 24.
- Доходность безрисковых государственных ценных бумаг (ГКО, ОФЗ в России, 10 летние облигации для США), которые обладают максимально возможной надежностью по рейтингам международных рейтинговых агентств Moody’s, Standard&poor’s и Fitch.
В результате необходимо сопоставить доходность полученную за счет управления рискованными ценными бумагами и минимальный уровень доходность абсолютно надежного актива.
Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс
Оценка паевого инвестиционного фонда по коэффициенту Шарпа
Оценка показателя Шарпа представлена в таблице ниже. К примеру, если показатель больше единицы, значит уровень избыточной доходности выше нежели существующий риск фонда или инвестиционного портфеля. Оценка показателя позволяет выбрать наиболее инвестиционно привлекательные фонды, портфели или стратегии для вложения.
| Значение показателя | Оценка эффективности управления |
| Sharp ratio >1 | Высокая результативность управления паевым инвестиционным фондом или портфелем. Данный фонд привлекателен для вложения |
| 1>Sharp ratio >0 | Уровень риска выше, нежели значение избыточной доходности паевого инвестиционного фонда. Необходимо рассмотреть другие показатели инвестиционной привлекательности фонда |
| Sharp ratio <0 | Уровень избыточной доходности отрицательный, целесообразнее вложить в безрисковый актив с минимальным уровнем риска |
| Sharp ratio1 > Sharp ratio2 | Первый паевой инвестиционный фонд более привлекателен для вложения, чем второй |
Вывод
В большинстве случаев, коэффициент Шарпа покажет реальную рентабельность стратегии. Но, иногда, показатель Шарпа может вводить в заблуждение. Например, некоторые облигации могут показывать стабильную доходность выше банковского процента в течении многих лет, на что коэффициент ответит нереалистично высокими показателями. В этом случае, полученное значение ничего не скажет о реальных рисках, стоящих за инвестированием в данную облигацию, пусть даже риск будет на самом деле минимальным. В целом же, данный коэффициент подойдёт для сравнения двух стратегий с относительно частыми входами и не самыми огромными целями.
С уважением, Алексей Вергунов TradeLikeaPro.ru
Пример выбра паевого инвестиционного фонда по коэффициенту Шарпа
Информацию о существующих фондах можно получить на сайте nlu.ru (национальная лига управляющих). Заходим на сайт и выбираем раздел «АНАЛИТИКА».→ «Коэффициент» → «Коэффициент Шарпа». В системе есть возможности отфильтровать по различным параметрам фонды: по типу, по управляющей компании, по категории и дате.
Оценка паевых инвестиционных фондов на основе коэффициента Шарпа
На рисунке ниже будет отражаться ранжирование всех паевых инвестиционных фондов по коэффициенту Шарпа. Так фонд «РЕГИОН Фонд акций» имеет максимальное значение коэффициента Шарпа, что свидетельствует о высоком качестве управления.
Оценка ПИФов на основе их эффективности управления
Пример оценки коэффициента Шарпа для инвестиционного портфеля
Если вы формируете сами инвестиционный портфель и вам необходимо сравнить различные портфели ценных бумаг, то для этого необходимо получить котировки изменения всех акций входящий в портфель, рассчитать их доходность и общий риск портфеля. Рассмотрим более подробно пример расчета коэффициента Шарпа в программе Excel.
Получить котировки можно с сайта finam.ru в разделе «Про рынок» → «Экспорт данных». Возьмем портфель из трех акций: ОАО «Газпром», ОАО «ГМК Норильский Никель» и ОАО «Сбербанк». Для каждой акции оценим долю в общем портфеле, так у Газпрома – 0,3, ГМК Нор. Никель – 0,5 и Сбербанк – 02. Для анализа брались котировки в течение года с 31.01.2014 – 31.01.2015.
Расчет коэффициента Шарпа для инвестиционного портфеля в Excel
На следующем этапе необходимо рассчитать доходность по каждой ценной бумаге портфеля. Для этого воспользуемся формулой в Excel:
Доходность акции Газпром =LN(B7/B6)
Доходность акции ГМК Нор. Никель =LN(C7/C6)
Доходность акции Сбербанк =LN(D7/D6)
Оценка доходности акций инвестиционного портфеля
Далее необходимо рассчитать параметры коэффициента: доходность и риск портфеля в целом, а также оценить безрисковую доходность. Доходность портфеля представляет собой взвешенную сумму среднеарифметических дневных доходностей, риск портфеля равен взвешенной сумме стандартных отклонений доходностей акций.
Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс
Безрисковая доходность была взята как годовая процентная ставка по депозиту в банке и составляет 12%. Воспользуемся следующими формулами оценки:
Доходность портфеля =СРЗНАЧ(E7:E256)*B4+СРЗНАЧ(F7:F256)*C4+СРЗНАЧ(G7:G256)*D4
Риск портфеля =СТАНДОТКЛОН(E7:E256)*B4+СТАНДОТКЛОН(F7:F256)*C4+СТАНДОТКЛОН(G7:G256)*D4
Коэффициент Шарпа =(H7-J7)/I7
Оценка эффективности инвестиционного портфеля по коэффициенту Шарпа
Как мы видим значения показателя Шарпа отрицательное, это говорит о том, что данный инвестиционный портфель сформирован неправильно и его следует пересмотреть. Доходность по безрисковому активу оказалась выше, чем сама доходность по акциям. Инвестору целесообразнее было вложиться в безрисковый актив нежели активно управлять и нести дополнительные риски. Более подробно узнать про коэффициенты оценки эффективности инвестиций вы можете в статье: “Оценка эффективности инвестиций, инвестиционного портфеля, акций на примере в Excel“.
Безрисковый доход
Безрисковкый доход – это теоретический доход с нулевым риском. То есть, это та доходность, которую инвестор может получить абсолютно без риска за какой-то определенный период времени. По идее, – это минимальный доход, который инвестор ожидает получить от любой инвестиции. Сравнивая этот показатель с реальным доходом, можно определить, насколько хорошую компенсацию вы получаете за дополнительный риск.
На практике, понятия инвестиции с нулевым риском не существует, так как даже самые безопасные инвестиции несут с собой некоторую долю риска. Тем не менее, к безрисковой доходности можно отнести депозит в сбербанке, либо деньги, инвестированные в казначейские облигации США. Рынок форекс – это всегда инвестиции с высоким риском, поэтому безрисковая доходность в нашем случае будет равна нулю. Но, если ваш депозит хранится в банке, в формулу можно подставить значение текущей базовой ставки.
В терминале MT4 показатель Шарпа считается, как отношение среднеарифметической доходности сделки к стандартному отклонению, при нулевом значении безрисковой ставки.
Полная формула выглядит так:
Модифицированный коэффициент Шарпа
Классический коэффициент Шарпа имеет ряд недостатков, которые решены в его модификации. Модификация показателя главным образом затрагивает изменение оценки риска инвестиционного портфеля. Для оценки риска используется не только стандартное отклонение как мера изменчивости доходности портфеля, а модифицированная мера риска VaR (Value at Risk). Данная мера позволяет оценить более реалистично будущие убытки за счет оценки характера распределения исторической доходности акций. Формула расчета его следующая:
где: rp – средняя доходность инвестиционного портфеля; rf – средняя доходность безрискового актива; σp – стандартное отклонение доходностей инвестиционного портфеля; S –эксцесс распределения доходностей; zc – куртозис распределения доходностей портфеля; K – квантиль распределения доходностей.
Оценка риска в данной модели основывается исключительно на статистическом расчете, что позволяет более адекватно оценить риски инвестиционного портфеля или паевого инвестиционного фонда.
| ★ Программа InvestRatio – расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса |
Сравнение Ex-Ante и Ex-Post Шарпа
Одним из преимуществ коэффициента Шарпа является маневренность при выборе типа данных о производительности для ввода в расчеты.
С одной стороны, коэффициент Шарпа можно использовать для оценки прошлых результатов инвестиций или портфеля. В этом случае фактические доходы используются в формуле.
Такое соотношение Шарпа называется «Ex-Post». Термин «Ex-Post» означает «после факта». Такое соотношение Шарпа может быть дополнительно использовано для прогнозирования будущих доходов от инвестиционного выбора с достаточными прошлыми данными.
В случае инвестиций или портфеля без адекватных прошлых данных о производительности инвестор может использовать ожидаемую производительность для расчета так называемого коэффициента Ex-Ante Шарпа.
Термин «Ex-Ante» означает «до факта», и такое соотношение Шарпа основано на оценках и / или прогнозируемых показателях.
Где применяется коэффициент Шарпа
Одним из направлений применения коэффициента Шарпа является сравнение и оценка эффективности инвестиционных портфелей, Фондов (ETF, REIT и др.), торговых стратегий. Сравнить инвестиционные портфели только по полученной доходности или только по риску (убыткам) не грамотно. Поэтому для определения результативности используется интегральный показатель, включающий доходность и риск. Чем выше значение коэффициента Шарпа, тем эффективнее инвестиционный портфель.
Смоделировать портфель можно в сервисе portfoliovisualizer.com. Для этого возьмем акции «большой четверки»: Apple (APPL), Google (GOOG), Amazon (AMZN), Facebook (FB). Первый портфель создадим без оптимизации весов акций. У каждой акции будет равный вес по 25%. Второй портфель оптимизируем по максимизации коэффициента Шарпа.
Максимизация коэффициента Шарпа позволяет найти оптимальные доли акций в портфеле
В оптимизированном портфеле изменятся веса акций ↓
| Тикер | Название | Вес нового портфеля |
| AMZN | Amazon. | 44.29% |
| GOOG | Alphabet | 5.43% |
| FB | 27.11% | |
| AAPL | Apple | 23.18% |
В таблице ниже представлены доходности и риски за 10-й период. Как видим, несмотря на небольшое увеличение волатильности портфеля, прибыльность выше.
| Портфель | Доходность за 10 лет | Риск (средняя волатильность) | Коэффициент Шарпа |
| Портфель с равными весами | 840% | 20,8% | 3,06 |
| Оптимизированный портфель | 1030% | 22,6% | 3,20 |
Наши портфели имеют коэффициент Шарпа больше 3, это говорит о том, что подобранные акции позволяют создавать доходность в 3 раза превышающую риски (выраженные в волатильности).
На рисунке ниже отражена динамика доходности первого и второго портфеля.
Оптимизация портфеля по коэффициенту Шарпа позволяет ребалансировать портфель, увеличит прибыль при незначительном увеличении риска
Относительность вычислений и результатов
Безусловно, коэффициент Шарпа достаточно наглядно иллюстрирует потенциал и риски. Но вместе с этим, есть случаи, когда эти цифры будут не очень адекватно показывать реальное положение дел и давать не совсем верную информацию, что в итоге приведёт к упущению больших возможностей по заработку.
Рассмотрим два простых случая, которые можно назвать рядовыми и которые часто встречаются на форексе и других финансовых рынках:
- Есть трейдер, который работает внутри дня, использует огромное кредитное плечо и депозит довольно сильно раскачивается в обе стороны. Если посмотреть на итоговый результат за месяц, то он может составлять десятки,а иногда и сотни процентов. Особенно часто это встречается у любителей криптовалюты, когда им удаётся поймать мощное движение, а также на волатильных кросс-парах валютного рынка, они могут пробегать за день по 500 пунктов. То есть результат выглядит потрясающим, но в реальности мы понимаем, что такая торговля не будет бесконечно успешной, рано или поздно депозит такого скальпера сливается. Происходит так по одной простой причине – если мы задействуем депозит полностью, то зарабатывать можем сколько угодно пунктов, а вот слив всегда будет через фиксированное значение. По евродоллару это будет около 110-120 пунктов при плече 1:100. Такой подход работы “на всё” практикуется многими. Коэффициент Шарпа будет очень высоким и будет показывать реальную картину.
- Есть трейдер, который реально много знает, умеет торговать и работает сразу по огромному количеству инструментов, но с малыми лотами. Нередко практикуется построение трендовых пирамид, то есть по мере движения в нужном направлении будет получаться постоянно растущий профит, а вот открытые ордера переводятся в безубыток. И так сразу по множеству инструментов. Стопы короткие, по возможности безубытки, зато профит удерживается до максимальных значений.
Что получаем в таком случае? Коэффициент Шарпа будет всё также высоким из-за высокой доходности, но вот только риски по факту совершенно другие. Слив такому трейдеру не грозит, у него рабочий подход совершенно другой, который предусматривает быструю фиксацию маленького по размеру убытка. А за счёт умений по тренду берутся огромные расстояния. Если посмотреть стейтмент, то там будет 70-80% убыточных и нулевых (безубыточных) сделок, но зато профитные будут в десятки раз больше по величине.
Вот и получается, что две одинаковые ситуации в рамках дохода и коэффициента Шарпа, а насколько всё отличается в реальной жизни. Именно поэтому не стоит смотреть на одни лишь цифры, нужно также обращать внимание на детали и изучать историю, смотреть ещё множество показателей. Это хорошо иллюстрируют ПАММ-сервисы, на которых можно перед инвестированием подробно изучить показатели счёта – какая максимальная просадка была, как выглядит кривая доходности и так далее. Всё это позволит принять верное решение и не вложиться в счёт, который завтра может слиться.