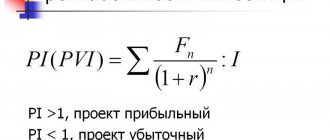It is necessary to evaluate business property for various reasons, for example, a future sale or an analysis of investment risks. You can add up the value of all owned assets to determine the value. But business is not only fixed assets; first of all, it is the income that they bring or can bring.
It is not enough to assess what kind of financial flow the enterprise and the property included in it can produce; it is also necessary to correlate these cash flows with the present time in order to determine whether the current price to be paid is reasonable with the projected profit in the future.
Let's take a closer look at the discounted cash flow (DCF) method used to assess the value of a business.
What are the features of managing an organization's cash flows ?
Discounting cash flows. Definition
cash flow (DCF, discounted value) is the reduction of the value of future (expected) cash payments to the current point in time. Discounting cash flows is based on the important economic law of diminishing value of money. In other words, over time, money loses its value compared to the current one, so it is necessary to take the current moment of assessment as the starting point and bring all future cash receipts (profits/losses) to the present time. For these purposes, a discount factor is used.
Take our proprietary course on choosing stocks on the stock market → training course
| Business valuation | Financial analysis according to IFRS | Financial analysis according to RAS |
| Calculation of NPV, IRR in Excel | Valuation of stocks and bonds |
How to calculate the discount rate?
★ Investment appraisal in Excel. Calculation of NPV, IRR, DPP, PI in 5 minutes The discount factor is used to reduce future income to the current value by multiplying the discount factor and payment streams. The formula for calculating the discount rate is shown below: where: r is the discount rate, i is the number of the time period.
Take our proprietary course on choosing stocks on the stock market → training course
| ★ InvestRatio program - calculation of all investment ratios in Excel in 5 minutes (calculation of Sharpe, Sortino, Treynor, Kalmar, Modiglanca beta, VaR ratios) + forecasting rate movements |
Discounting cash flows. Calculation formula
where: DCF (Discounted cash flow) – discounted cash flow; CF (Cash Flow) – cash flow in time period I; r – discount rate (rate of return); n is the number of time periods for which cash flows appear. The key element in the cash flow discounting formula is the discount rate. The discount rate shows what rate of return an investor should expect when investing in a particular investment project. The discount rate uses many factors that depend on the object of evaluation, and may include: the inflation component, return on risk-free assets, additional rate of return for risk, refinancing rate, weighted average cost of capital, interest on bank deposits, etc.
Discounting and investment projects
This means that an investor who invests financial resources in an idea receives not engineering or human resources in the form of a group of first-class experts, new offices, bases, high-tech equipment, etc., but tomorrow’s influx of finance . If we continue to develop this topic, it turns out that various businesses “produce only one product to the market - money.
The main advantage of the method of discounting financial assets is that this method of analysis, only one of all the current ones, is aimed at market prospects, this helps the development of investment.
Calculation of rate of return (r) for discounting cash flows
Take our proprietary course on choosing stocks on the stock market → training course
There are quite a lot of different ways and methods for estimating the discount rate (rate of return) in investment analysis. Let us consider in more detail the advantages and disadvantages of some methods for calculating the rate of return. This analysis is presented in the table below.
| Methods for estimating discount rates | Advantages | Flaws |
| CAPM models | Ability to take into account market risk | One-factor, the need for the presence of ordinary shares on the stock market |
| Gordon model | Easy calculation | The need for ordinary shares and constant dividend payments |
| Weighted average cost of capital (WACC) model | Accounting for the rate of return of both equity and debt capital | Difficulty in estimating return on equity |
| Model ROA, ROE, ROCE, ROACE | Ability to take into account the return on capital of a project | Not taking into account additional macro and micro risk factors |
| E/P method | Taking into account the market risk of the project | Availability of quotes on the stock market |
| Method for estimating risk premiums | Using additional risk criteria in assessing the discount rate | Subjectivity of risk premium assessment |
| Assessment method based on expert opinions | The ability to take into account poorly formalized project risk factors | Subjectivity of expert assessment |
You can learn more about approaches to calculating the discount rate in the article “Discount rate. 10 modern valuation methods.”
| ★ InvestRatio program - calculation of all investment ratios in Excel in 5 minutes (calculation of Sharpe, Sortino, Treynor, Kalmar, Modiglanca beta, VaR ratios) + forecasting rate movements |
Internal rate of return (IRR)
IRR is another project evaluation method using DCF methods.
IRR is the discount rate at which the NPV of an investment is zero. Thus, it represents the breakeven cost of capital.
Calculating IRR using linear interpolation
Steps in linear interpolation:
- Calculate two NPVs for a project at two different capital costs
- Use the following formula to find the IRR:
Where:
L = lower interest rate H = higher interest rate NL = NPV at a lower interest rate NH = NPV at a higher interest rate.
The chart below shows the IRR estimated by the formula.
Decision Rule:
- projects should be accepted if their IRR is greater than the cost of capital.
Example of using IRR
The projected cash flows of the potential project give an NPV of $50,000 at a discount rate of 10% and an NPV of $10,000 at a discount rate of 15%.
Calculate the IRR.
Solution:
IRR = 14.17%
Advantages and Disadvantages of IRR
Advantages
IRR has a number of advantages, e.g. This:
- takes into account the time value of money
- is percentage and therefore easy to understand
- uses cash flows without profit
- considers the entire life of the project
- means that the firm selects projects in which the IRR exceeds the cost of capital should increase shareholder wealth.
Flaws
- This is not a measure of absolute profitability.
- Interpolation provides only an estimate, and an accurate estimate requires the use of a spreadsheet program.
- This is quite difficult to calculate.
- Unconventional cash flows may result in multiple IRRs, which means that the interpolation method cannot be used.
Difficulties with the IRR approach
Interpolation only provides an estimate (and an accurate estimate requires the use of a spreadsheet program). The cost of capital calculation itself is also only a rough estimate, and if the difference between the required return and the IRR is small, then this lack of precision may actually mean that the wrong decision is being made.
Another disadvantage of IRR is that non-traditional cash flows can result in no IRR or multiple IRRs. For example, a project with outflows in T0 and T2 but income in T1 could, depending on the size of the cash flows, have several different profiles on different graphs (see below). Even where a project has a single IRR, the graph shows that the acceptance rule will lead to the wrong result because the project does not receive a positive NPV at any cost of capital.
Example of calculating discounted cash flow in Excel
In order to calculate discounted cash flows, it is necessary to describe in detail all expected positive and negative cash payments for a selected time period (in our case, annual intervals) (CI - Cash Inflow, CO - Cash Outflow). The following payments are taken for cash flows in valuation practice:
- Net operating income;
- Net cash flow excluding operating costs, land tax and reconstruction of the facility;
- Taxable income.
In domestic practice, as a rule, a period of 3-5 years is used; in foreign practice, the assessment period is 5-10 years. The entered data is the basis for further calculations. The figure below shows an example of entering initial data into Excel.
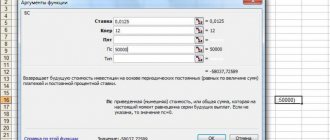
Discounted Cash Flow (DCF) calculation in Excel
At the next stage, cash flow is calculated for each of the time periods (column D). One of the key tasks of assessing cash flows is calculating the discount rate, in our case it is 25%. And it was obtained using the following formula: Discount rate = Risk-free rate + Risk premium The key rate of the Central Bank of the Russian Federation was taken for the risk-free rate. The key rate of the Central Bank of the Russian Federation is currently 15% and the premium for risks (production, technological, innovative, etc.) was calculated by experts at the level of 10%. The key rate reflects the return on a risk-free asset, and the risk premium shows the additional rate of return on the existing risks of the project. You can learn more about calculating the risk-free rate in the following article: “Risk-free rate of return. 5 modern methods of calculation" Then it is necessary to bring the received cash flows to the initial period, that is, multiply them by the discount factor. As a result, the sum of all discounted cash flows will give the discounted value of the investment object. The calculation formulas will be as follows: Cash Flow (CF) = B6-C6 Discounted Cash Flow (DCF) = D6/(1+$C$3)^A6 Total Discounted Cash Flow (DCF) = SUM(E6:E14)
Discounting cash flows, valuation example in Excel
As a result of the calculation, we received the discounted value of all cash flows (DCF) equal to RUB 150,981. This cash flow has a positive value, which indicates the possibility of further analysis. When conducting an investment analysis, it is necessary to compare the final values of discounted cash flow for various alternative projects, this will allow them to be ranked according to the degree of attractiveness and efficiency in creating value.
IFRS, Dipifr
Do you know what discounting means? If you are reading this article, then you have already heard this word. And if you haven’t yet fully understood what it is, then this article is for you. Even if you are not going to take the Dipifr exam, but just want to understand this issue, after reading this article, you will be able to clarify the concept of discounting for yourself.
This article explains in accessible language what discounting is. It shows the technique of calculating discounted value using simple examples. You will learn what a discount factor is and how to use discount factor tables.
The concept and formula of discounting in accessible language
To make it easier to explain the concept of discounting, let's start from the other end. Or rather, let’s take an example from life that is familiar to everyone.
Example 1.
Imagine that you went to the bank and decided to make a deposit of $1,000. Your 1000 dollars deposited in the bank today, at a bank rate of 10%, will be worth 1100 dollars tomorrow: the current 1000 dollars + interest on the deposit 100 (= 1000 * 10%). In total, after a year you will be able to withdraw $1,100. If we express this result through a simple mathematical formula, we get: $1000*(1+10%) or $1000*(1.10) = $1100.
In two years, the current $1,000 will become $1,210 ($1,000 plus first year interest $100 plus second year interest $110=1100*10%). The general formula for increasing the contribution over two years: (1000*1.10)*1.10 = 1210
Over time, the amount of the contribution will continue to grow. To find out what amount is due to you from the bank in a year, two, etc., you need to multiply the deposit amount by the multiplier: (1+R)n
- where R is the interest rate, expressed in fractions of a unit (10% = 0.1)
- N – number of years
In this example, 1000 * (1.10)2 = 1210. It is obvious from the formula (and from life too) that the deposit amount after two years depends on the bank interest rate. The larger it is, the faster the contribution grows. If the bank interest rate were different, for example, 12%, then after two years you would be able to withdraw approximately $1,250 from the deposit, and if we calculate more precisely, 1,000 * (1.12)2 = 1,254.4
In this way, you can calculate the amount of your contribution at any point in time in the future. Calculating the future value of money in English is called “compounding”. This term is translated into Russian as “extension” or by tracing paper from English as “compounding”. Personally, I prefer the translation of this word as “increment” or “increase”.
The meaning is clear - over time, the cash deposit increases due to the increment (growth) of annual interest. In fact, the entire banking system of the modern (capitalist) model of the world order, in which time is money, is built on this.
Now let's look at this example from the other end. Let's say you need to repay a debt to your friend, namely: in two years you need to pay him $1210. Instead, you can give him $1,000 today, and your friend will deposit this amount in the bank at an annual rate of 10% and in two years withdraw exactly the required amount of $1,210 from the bank deposit. That is, these two cash flows: $1000 today and $1210 in two years are equivalent
each other. It doesn't matter what your friend chooses - these are two equal possibilities.
EXAMPLE 2.
Let's say in two years you need to make a payment in the amount of $1,500. What will this amount be worth today?
To calculate today's value, you need to go from the opposite: $1500 divided by (1.10)2, which will be equal to approximately $1240. This process is called discounting.
In simple terms, discounting is the determination of the present value of a future amount of money (or, more correctly, a future cash flow).
If you want to find out how much a sum of money you either receive or plan to spend in the future will cost today, then you need to discount that future amount at a given interest rate. This rate is called the "discount rate."
In the last example, the discount rate is 10%, $1,500 is the payment amount (cash outflow) in 2 years, and $1,240 is the so-called
discounted value of future cash flow.
In English, there are special terms to denote today's (discounted) and future value: future value (FV) and present value (PV). In the example above, $1500 is the future value of FV and $1240 is the present value of PV. When we discount, we go from the future to today.
Discounting
When we build up, we move from today to the future.
Extension
The formula for calculating the present value or discounting formula for this example is: 1500 * 1/(1+R)n = 1240.
The mathematical discounting formula in the general case will be as follows: FV * 1/(1+R)n = PV. It is usually written like this:
PV = FV * 1/(1+R)n
Coefficient by which the future value is multiplied 1/(1+R)n
called a discount factor from the English word factor meaning “coefficient, multiplier”.
In this discounting formula: R is the interest rate, N is the number of years from a date in the future to the current moment.
Thus:
- Compounding or Increment is when you go from today's date to the future.
- Discounting or Discounting is when you go from the future to today.
Both “procedures” allow us to take into account the effect of changes in the value of money over time.
Of course, all these mathematical formulas immediately make the average person feel sad, but the main thing is to remember the essence. Discounting is when you want to know the present value of a future amount of money (that you will need to spend or receive).
I hope that now that you have heard the phrase “concept of discounting,” you can explain to anyone what is meant by this term.
Is present value the discounted value?
In the previous section we found out that
Discounting is the determination of the present value of future cash flows.
Isn’t it true that in the word “discounting” you hear the word “discount” or discount in Russian? And indeed, if you look at the etymology of the word discount, then already in the 17th century it was used in the meaning of “deduction for early payment,” which means “discount for early payment.” Even then, many years ago, people took into account the time value of money. Thus, one more definition can be given: discounting is the calculation of a discount for prompt payment of bills. This “discount” is a measure of the time value of money.
Present value is the present value of a future cash flow (i.e., the future payment minus the “discount” for prompt payment). It is also called present value, from the verb “to bring.” In simple terms, present value is the future amount of money given
to the current moment.
To be precise, discounted and present value are not absolute synonyms. Because you can bring not only the future value to the current moment, but also the current value to some point in the future. For example, in the very first example, we can say that $1,000 discounted to the future (two years from now) at a 10% interest rate is equal to $1,210. That is, I want to say that present value is a broader concept than discounted value.
By the way, in English there is no such term (present value). This is our, purely Russian invention. In English there is the term present value (current value) and discounted cash flows (discounted cash flows). And we have the term present value, and it is most often used in the sense of “discounted” value.
Discount table
A little higher I already gave the discounting formula PV = FV * 1/(1+R)n , which can be described in words as:
Present value equals future value multiplied by a factor called the discount factor.
The discount factor 1/(1+R)n, as can be seen from the formula itself, depends on the interest rate and the number of time periods. In order not to calculate it each time using the discounting formula, use a table showing the values of the coefficient depending on the percentage of the rate and the number of time periods. It is sometimes called a "discount table", although this is not the correct term. This is a table of discount factors , which are calculated, as a rule, accurate to the fourth decimal place.
Using this table of discount factors is very simple: if you know the discount rate and the number of periods, for example, 10% and 5 years, then at the intersection of the corresponding columns you will find the coefficient you need.
Example 3.
Let's look at a simple example. Let's say you need to choose between two options:
- A) get $100,000 today
- B) or $150,000 in one amount exactly in 5 years
What to choose?
If you know that the bank rate on 5-year deposits is 10%, then you can easily calculate what the amount of $150,000 due in 5 years is equal to today.
The corresponding discount factor in the table is 0.6209 (the cell at the intersection of the 5 years row and the 10% column). 0.6209 means that 62.09 cents received today equals $1 received in 5 years (at 10% interest). Simple proportion:
| Today | after 5 years |
| 62.09 cents | $1 |
| X? | 150,000 |
So $150,000*0.6209 = 93.135.
93,135
is the discounted (present) value of the amount of $150,000 to be received in 5 years.
It's less than $100,000 today. In this case, a bird in the hand is really better than a pie in the sky. If we take $100,000 today and put it on deposit in a bank at 10% per annum, then in 5 years we will receive: 100,000*1.10*1.10*1.10*1.10*1.10 = 100,000*( 1.10)5 = $161,050. This is a more profitable option.
To simplify this calculation (calculating future value given today's value), you can also use a coefficient table. By analogy with the discount table, this table can be called a table of increment (accretion) factors. You can build such a table yourself in Excel if you use the formula to calculate the increment factor: (1+R)n
.
From this table it can be seen that $1 today at a rate of 10% will cost $1.6105 in 5 years.
Using such a table, it will be easy to calculate how much money you need to put in the bank today if you want to receive a certain amount in the future (without replenishing the deposit). A slightly more complicated situation arises when you not only want to deposit money today, but also intend to add a certain amount to your deposit every year. How to calculate this, read the next article. It's called the annuity formula.
A philosophical digression for those who have read this far
Discounting is based on the famous postulate “time is money”
. If you think about it, this illustration has a very deep meaning. Plant an apple tree today and in a few years your apple tree will grow and you will be picking apples for years to come. And if you don’t plant an apple tree today, then in the future you will never try apples.
All we need is to decide: to plant a tree, start our own business, take the path leading to the fulfillment of our dreams. The sooner we take action, the greater the harvest we will get at the end of the journey. We need to turn the time we have in our lives into results.
“The seeds of flowers that will bloom tomorrow are planted today.”
That's what the Chinese say.
If you dream about something, don't listen to those who discourage you or question your future success. Don't wait for a lucky coincidence of circumstances, start as early as possible. Turn the time of your life into results.
Large table of discount rates (opens in a new window):
You can read other articles on the topic of Finance:
1. Deposit capitalization - what is it? Interest capitalization formula: monthly, daily, continuous. You can calculate your potential income on a deposit yourself, without relying on income calculators that are posted on the websites of banking institutions. This article shows, using specific examples, how to calculate income on a deposit with interest capitalization (quarterly, monthly) and how to calculate the effective rate on deposits with capitalization.
2. Annuity formula. Perpetual annuity. Everyone needs to know this! (not for bankers) A perpetual annuity is a series of equal payments that continue forever. This option is possible if, for example, you have a deposit in a bank, you withdraw only annual interest, and the principal amount of the deposit remains untouched. Then, if the interest rate on the deposit does not change, you will have a so-called perpetual annuity.
3. Formula for calculating the NPV of an investment project. It's simple.
Investing means investing free financial resources today in order to obtain stable cash flows in the future. How not to make a mistake and not only return the invested funds, but also get a profit from the investment?
4. Internal rate of return. Formula for calculating IRR of an investment project
This article provides not only the formula and definition of IRR, but there are examples of calculations of this indicator (in Excel, graphical) and interpretation of the results obtained. Two examples from life that every person encounters
5. Discount rate for an investment project. This is WACC - weighted average cost of capital.
At its core, the discount rate when analyzing investment projects is the interest rate at which the investor attracts financing. How to calculate it?
The most interesting articles on the topic of IFRS and Dipifra:
1. Consolidation is control. IFRS 10 is a common control concept for all business combinations
2. How to pass the Dipifr exam the second time?
Go to home page
Investment analysis methods using discounted cash flows
It should be noted that discounted cash flow (DCF) in its calculation formula is very similar to net present value (NPV). The main difference is the inclusion of initial investment costs in the NPV formula. Discounted cash flow (DCF) is used in many methods for assessing the effectiveness of investment projects. Because these methods use discounting of cash flows, they are called dynamic.
- Dynamic methods for evaluating investment projects Net present value (NPV, Net Present Value)
- Internal rate of return (IRR, Internal Rate of Return)
- Profitability index (PI, Profitability index)
- Equivalent annuity (NUS, Net Uniform Series)
- Net rate of return (NRR, Net Rate of Return)
- Net Future Value (NFV, Net Future Value)
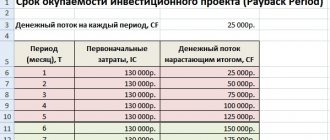
- Discounted Payback Period (DPP, Discounted Payback Period)
You can learn more about methods for calculating the effectiveness of investment projects in the article “6 methods for assessing the effectiveness of investments in Excel. An example of calculating NPV, PP, DPP, IRR, ARR, PI.” In addition to just discounting cash flows, there are more complex methods that in addition take into account the reinvestment of cash payments.
- Modified Net Rate of Return (MNPV)
- Modified Internal Rate of Return (MIRR)
- Modified net present value (MNPV, Modified Present Value)
| ★ InvestRatio program - calculation of all investment ratios in Excel in 5 minutes (calculation of Sharpe, Sortino, Treynor, Kalmar, Modiglanca beta, VaR ratios) + forecasting rate movements |
Advantages and disadvantages of the DCF indicator for discounting cash flows
+) The use of a discount rate is an undoubted advantage of this method, since it allows you to reduce future payments to the current value and take into account possible risk factors when assessing the investment attractiveness of the project. -) The disadvantages include the difficulty of predicting future cash flows for an investment project. In addition, it is difficult to reflect changes in the external environment in the discount rate. Summary Discounting cash flows is the basis for calculating many coefficients for assessing the investment attractiveness of a project.
We have analyzed, using an example, the algorithm for calculating discounted cash flows in Excel, their existing advantages and disadvantages. Ivan Zhdanov was with you, thank you for your attention. Author: Ph.D. Zhdanov Ivan Yurievich
| Business valuation | Financial analysis according to IFRS | Financial analysis according to RAS |
| Calculation of NPV, IRR in Excel | Valuation of stocks and bonds |
Net Present Value (NPV)
To estimate the overall impact of a project using DCF methods, it involves discounting all relevant cash flows associated with the project to their present value (PV).
If we consider the outflows of a project as negative and the inflows as positive, the NPV of a project is the sum of the present values (PV) of all the flows resulting from the project.
Decision Rule:
NPV represents the surplus (after investment financing) earned by the project, therefore:
- if the NPV is positive, the project is financially viable
- if NPV is zero, the project even breaks down
- if the NPV is negative, the project is not financially viable
- if a company has two or more mutually exclusive projects, they should choose the one with the highest NPV
Assumptions in calculating net present value
In calculating net present value, the following cash flow assumptions are made:
- all cash flows occur at the beginning or end of the year
- initial investment occurs T0
- other cash flows begin one year after that (T1).
Also, interest payments are never included in the NPV calculation because they are accounted for at the cost of capital.
Example of using NPV
An organization is considering investment in new equipment. The estimated cash flows are as follows.
The company's cost of capital is 9%.
Calculate the NPV of a project to evaluate whether it should be pursued . Solution:
The PV of cash inflows exceeds the PV of cash outflows by $29,760, meaning the project will earn a DCF return of more than 9%, meaning it will earn a surplus of $29,760 after paying the cost of financing. Therefore it should be carried out.