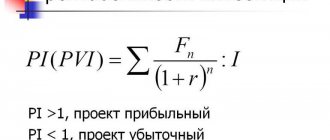Коэффициент бета. Определение
Коэффициент бета (англ. Beta, β, beta coefficient) – определяет меру риска акции (актива) по отношению к рынку и показывает чувствительность изменения доходности акции по отношению к изменению доходности рынка. Коэффициент бета может быть рассчитан не только для отдельной акции, но также и для инвестиционного портфеля. Коэффициент используется как мера систематического риска, и применяется в модели У.Шарпа – оценки капитальных активов CAPM (Capital Assets Price Model). В первые, коэффициент бета рассмотрел Г. Марковиц для оценки систематического риска акций, который получил называние индекс недиверсифицируемого риска. Коэффициент бета позволяет сравнивать между собой акции различных компаний по степени их риска.
Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс
Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс
Бета инвестиционного портфеля
До этого мы говорили о бете отдельного актива. Но если говорить о бете инвестиционного портфеля, то тут немного другая картина.
Современная портфельная теория предполагает, что рынок эффективен: вся информация тут же закладывается в цену акции, и ни один участник рынка не может получить преимущество над другим. Следовательно, единственный способ получения доходности выше рынка – взять на себя больший риск.
А вот еще интересная статья: Трейдинг, активное и пассивное инвестирование – что это и чем они отличаются?
Какой именно риск готов принять инвестор, и показывает бета портфеля. Если бета портфеля больше единицы, то он (портфель) будет более доходным, но в кризис будет проваливаться сильнее, чем индекс. Если бета меньше 1, то инвестор будет недополучать доход, но его портфель в кризис будет вести себя устойчивее.
Следовательно, суть портфельного инвестировать – собрать портфель с такой бетой, которая бы устроила инвестора.
Консервативным инвесторам достаточно беты равной 1 или даже меньше 1. А агрессивным подавай бету побольше и пожирнее )))
Как будет выглядеть формула беты портфеля? Суть такая же, как для одной акции, но в портфеле у нас несколько активов, поэтому нужно учитывать их веса. Это логично. Если портфель на 95% состоит из акций и на 5% из облигаций, то облигации внесут малый вклад в стабилизацию беты.
Поэтому бета портфеля – это просто сумма бет отдельных активов с модификатором их веса:
Здесь:
- Вр– бета всего портфеля;
- Вn– бета n-ой акции;
- W – вес акции;
- n – число элементов (акций) в портфеле.
Ожидаемую доходность портфеля тоже можно выразить через бету. Для этого используют такую формулу:
Здесь:
- Ep– ожидаемая доходность;
- Er– доходность рынка (индекса).
В курсе «Как составить свой инвестиционный портфель» я подробно объясняю, как вам самим подсчитать бету, где можно найти готовые расчеты коэффициентов альфа и бета для отдельных активов и самое главное: как с помощью автоматизированных сервисов составить портфель с оптимальной бетой и другими мультипликаторам (например, коэффициентом Шарпа). Если вы приверженец индексного инвестирования – эта информация будет для вас бесценна.
Итак, бета – это коэффициент, который измеряет изменчивость актива по отношению к индексу (бенчмарку). Бету считают как для отдельной бумаги, так и для всего портфеля в целом. Консервативным инвесторам лучше выбирать акции и собирать портфели с бетой, близкой к 1. А агрессивным можно и рискнуть. Удачи, и да пребудут с вами деньги!
Оцените статью
[Общее число голосов: 2 Средняя оценка: 5]
Формула расчета коэффициента бета
где:
β – коэффициент бета, мера систематического риска (рыночного риска);
ri – доходность i-й акации (инвестиционного портфеля);
rm – рыночная доходность;
σ2m – дисперсия рыночной доходности.
| ★ Excel таблица для формирования инвестиционного портфеля ценных бумаг (рассчитай портфель за 1 минуту) + оценка риска и доходности |
| ★ Программа InvestRatio – расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса |
Коэффициент Сортино
Коэффициент Сортино, так же как и коэффициент Шарпа, характеризует эффективность управления фондом с точки зрения сочетания доходности и риска. Но расчет риска здесь базируется не на всех колебаниях результатов фонда относительно средней доходности (стандартное отклонение), а только на отрицательных колебаниях.
Формула расчета коэффициента Сортино на отрезке в 3 года:
Sortino Ratio = (y – r)/36/σ’,
где y – значение доходности фонда за 36 месяцев, предшествующих дате расчета;
r – процентная ставка по депозитам в рублях для населения за 36 месяцев(ставка безрискового актива);
σ’ – стандартное отклонение (волатильность) отрицательной доходности фонда за 36 месяцев. Из базы расчета исключаются данные положительной доходности фонда.
Анализ уровня риска по значению коэффициента бета (β)
Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс
Коэффициент бета показывает рыночный риск акции и отражает чувствительность изменения акции по отношению к изменению доходности рынка. В таблице ниже показана оценка уровня риска по коэффициенту бета. Коэффициент бета может иметь как положительный, так и отрицательный знак, который показывает положительную или отрицательную корреляцию между акцией и рынком. Положительный знак отражает, что доходность акций и рынка изменяются в одном направлении, отрицательный – разнонаправленное движение.
| Значение показателя | Уровень риска акции | Направление изменения доходности акции |
| β > 1 | Высокий | Однонаправленное |
| β = 1 | Умеренный | Однонаправленное |
| 0 < β < 1 | Низкий | Однонаправленное |
| -1 < β < 0 | Низкий | Разнонаправленное |
| β = -1 | Умеренный | Разнонаправленное |
| β < -1 | Высокий | Разнонаправленное |
В статье дано описание бета-коэффициента и бета-нейтрального (рыночно-нейтрального) инвестиционного портфеля. Продолжает цикл публикаций о приложении методов теории вероятности и математической статистики к операциям с ценными бумагами и другими финансовыми активами.
СОДЕРЖАНИЕ:
1. Бета-коэффициент ценной бумаги 2. Пример расчета Бета-коэффициента акции 3. Бета-коэффициент и риск портфеля ценных бумаг 4. Пример расчета Бета-коэффициента портфеля акций 5. Бета-нейтральный портфель и парный трейдинг Примечания и ссылки Используемые сокращения
1. БЕТА-КОЭФФИЦИЕНТ ЦЕННОЙ БУМАГИ
В конце прошлого века американский экономист, лауреат Нобелевской премии по экономике 1990 г. Уильям Форсайт Шарп (William Forsyth Sharpe) сделал допущение о линейной зависимости между среднерыночной доходностью (доходностью фондового индекса) и доходностью отдельно взятой ценной бумаги (ЦБ). Им была предложена следующая формула для расчета доходности ЦБ[]:
Исходя из линейности связи между доходностью акции и индекса, У. Шарп предположил, что между этими случайными величинами имеет место полная корреляция, то есть, корреляционная зависимость с коэффициентом корреляции по модулю равным единице.
Уильям Ф. Шарп[]
Таким образом, доходность отдельной ценной бумаги (акции) по формуле 1 содержит три слагаемых.
Первое, Альфа-коэффициент или коэффициент смещения, характеризует «собственный, несистематический» вклад по конкретной акции. Вторая компонента, равная произведению коэффициента, называемого Бета-коэффициентом или коэффициентом наклона, на доходность фондового индекса RI, отражает «систематическое, рыночное» влияние на доходность данной бумаги. Наконец, третий член правой части уравнения, ε, дает размер погрешности по i-ой акции, применение которого позволяет замкнуть в равенство первые два слагаемых слева и доходность акции справа.
Безусловно, формула 1 лучше работает для индексной бумаги. То есть для акции, входящей в корзину индекса RI. Тогда ri логично записать, как riI.
Интерпретировать спектр значений Бета-коэффициента (далее коротко по тексту «Бета») можно так:
- Бета<0 – обратная корреляция между доходностью акции и индекса, т.е. при увеличении RI, ri падает и наоборот.
- Бета=0 нет корреляции между акцией и выбранным индексом.
- 0<�Бета<1 – прямая зависимость, волатильность (степень изменчивости) акции меньше волатильности индекса.
- Бета=1 – четкая прямая связь между акцией и индексом. Волатильности акции и индекса одинаковы.
- Бета>1 – прямая зависимость, положительная корреляция. Волатильность индекса выше волатильности данной акции.
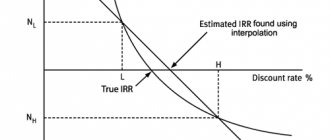
Как ведет себя Бета при двух различных положительных значениях, хорошо иллюстрируются ниже приведенными рисунками[] (ε принимается равным 0):
Для акции А: Бета=1,2 (>1), Альфа положителен и равен 2%. Для акции В: Бета=0,8 (<1), Альфа отрицателен и равен минус 1%. Из элементарной геометрии Бета – тангенс угла наклона прямой к оси абсцисс. Отсюда и второе название Бета – коэффициент наклона.
Больший угол наклона прямой для акции А к оси абсцисс (RI) обуславливает более резкое изменение ri при изменении RI, по сравнению с прямой для акции В. Кроме того, дан наглядный геометрический смысл Альфа-коэффициентов. Они дают значения ri при RI=0.
Бета рассчитывается следующим образом:
Что такое ковариация, дисперсия и среднеквадратичное отклонение (СКО) было подробно объяснено во вводной статье «Основы теории вероятностей для инвестора. От понятия вероятности до нормального распределения». Из формулы очевидно, что Бета не имеет размерности.
2. ПРИМЕР РАСЧЕТА БЕТА-КОЭФФИЦИЕНТА АКЦИИ
Определим Бета для акций Apple, на 22.03.19 крупнейшей в мире публичной компании по капитализации ($923 млрд)[]. Главная торговая площадка – биржа NASDAQ. Тикер AAPL. Бумага входи в корзину ключевых американских индексов – DJIA (промышленный индекс Доу-Джонс) и S&P500.
В качестве временного периода выберем закончившийся 2021 год. Снимем[] 15 значений цен закрытия AAPL за первое число каждого месяца с 01.12.17 по 01.02.19 включительно и соответствующие им значения S&P500.
Доходность (помесячную) акции и индекса (в %) посчитаем так:
(Sпосл-Sпред)/Sпред*100.
Здесь Sпред – предыдущее значение величины (цена акции или значение индекса), Sпосл – ее последующее значение.
Сведем полученные результаты в таблицу:
Желтый цвет отвечает акциям AAPL, зеленый – индексу S&P500.
Далее, в Excel применим к колонкам доходностей функцию КОВАР из раздела «Статистические». Получим значение ковариации cov(AAPL,S&P500)=16,344. Для вычисления дисперсии D(RI) можно использовать две формулы Excel из того же раздела статфункций: ДИСП и ДИСПР. Первая посчитает дисперсию для отдельной выборки, вторая – для генеральной совокупности значений. Что такое выборка и генеральная совокупность, и в чем их отличие, также смотрите в упомянутой выше статье нашего сайта «Основы теории вероятностей для инвестора…».
Делим ковариацию на дисперсии и получаем Бета, отдельно по выборке, Бета(выб.)=0,744 и по генеральной совокупности, Бета(гс)=0,802.
Получается, что акции AAPL (по генеральной совокупности) ведут себя по отношению к индексу S&P500 на рассматриваемом периоде, с выбранной (помесячной) частотой, почти, как акции В из примера предыдущего раздела (см. рисунок). Альфа-коэффициент не учитываем.
3. БЕТА-КОЭФФИЦИЕНТ И РИСК ПОРТФЕЛЯ ЦЕННЫХ БУМАГ
Формула для расчета Бета-коэффициента портфеля ценных бумаг (акций) имеет вид:
Бета связывает не только доходности бумаги и индекса (эталонного портфеля), но и риски отдельной ценной бумаги (ЦБ) и индекса. Напомним, что под риском ЦБ понимают дисперсию ее доходности (D) или СКО (σ)[]: D=σ2.
В соответствии с «рыночной моделью» [] полные риски бумаги и портфеля, в целом, записываются следующим образом:
Общий риск отдельной акции и всего портфеля зависит от рыночного риска (первое слагаемое βiI2σI2 для акции или βpI2σI2 для портфеля) и от собственного риска (второе слагаемое σεi2 для акции и σεp2 для портфеля).
Даже начинающий инвестор знает, что уменьшить суммарный риск по портфелю можно, проведя его максимальную диверсификацию. Увеличивая число акций различных компаний, трейдер смягчает негативное воздействие от неудач в отдельных позициях. Идеальным является случай, когда набор ЦБ полностью копирует индексную корзину, например, S&P500. Тогда β портфеля равно 1 (с учетом погрешности вычислений) и общий риск портфеля σp2 обусловлен только рыночным риском σI2.
Переход общего риска портфеля в рыночный риск, при увеличении числа представленных в нем компаний, демонстрирует график[]:
4. ПРИМЕР РАСЧЕТА БЕТА-КОЭФФИЦИЕНТА ПОРТФЕЛЯ АКЦИЙ
Согласно формуле 3, для расчета Бета портфеля надо знать Бета каждой акции (компании) и ее удельный вес в портфеле.
Допустим, необходимо определить на 01.02.2019 г. Бета портфеля, состоящего из рассмотренного выше Apple (AAPL), а также Microsoft (MSFT), Amazon (AMZN) и Facebook (FB). Эталоном вновь выбираем S&P500, временной период и частота съема информации, аналогичны примеру с Apple: котировки за первое число каждого месяца с 01.12.17 по 01.02.19.
Предположим, предпочтения инвестора по структуре портфеля таковы: 50% — AMZN, 25% — MSFT, 15% — AAPL и 10% — FB. Пусть, всего инвестировано $1 млн, тогда в AMZN вложено 0,5 млн, в MSFT – 0,25 млн, AAPL – 0,15 млн и в FB – 0,1 млн долларов.
Воспользуемся уже имеющимся массивом для AAPL и S&P500 и вытащим[] соответствующие котировки для AMZN, MSFT и FB.
Обработаем котировки акций и значения S&P500, как это было сделано при расчете Бета для Apple выше. Сделаем допущение о том, что наши данные – генеральная совокупность помесячных значений исследуемых величин в интервале 01.12.17-01.02.19.
Сведем результаты в следующую таблицу:
В желтом секторе таблицы высчитаны ковариации доходности акций относительно доходности S&P500. В зеленом поле –дисперсия доходностей S&P500 (уже рассчитывалась ранее). В голубом поле – Бета по каждой акции, равное отношению соответствующей ковариации к дисперсии доходности индекса. Наконец, в нижней строке таблицы итоговая Бета портфеля, исходя из весов каждой акции (компании).
Видно, что наиболее близко по доходности к индексу идет Microsoft (Бета=1,03), наиболее далек – Facebook (Бета=1,98). На прирост/падение доходности S&P500 на 1% акции компании Цукерберга реагируют на 2%.
Портфель с Бета=1,52 достаточно агрессивен – уровень риска на 52% выше среднерыночного по S&P500.
Как должен поступить инвестор, стремящийся снизить риск портфеля до среднерыночного (индексного), оперируя данными четырьмя эмитентами?
С одной стороны казалось бы, проще всего, наполнить весь портфель исключительно акциями MSFT с Бета=1,03. Но как же быть тогда с диверсификацией?
Исходя из Бета-коэффициентов, можно предложить увеличить удельный вес эмитентов в с Бета близкими к 1 и уменьшить вес бумаг, с Бета от 1 далекими. Например, структура портфеля с 50% MSFT, 30% AAPL, 15% AMZN и 5% FB даст общую Бета портфеля в 1,14. При этом, будет сохранена возможность неплохо заработать на резких движениях вверх AMZN и FB при росте доходности индекса.
Формируя портфель надо помнить и о дивидендах по акциям. В нашей модели, на анализируемом периоде, акционеров радовали Apple: три квартальные выплаты по $0,73 и одна $0,63 на акцию; и Microsoft: трижды по 42 цента и один раз по 46 центов на акцию.
Много это или мало? Суммарный дивиденд за рассматриваемый год по Apple – $2,82 на акцию, по Microsoft – $1,72 на акцию. Сравним с ценой акций на начало инвестирования (01.01.18) – Apple стоил $167,43, Microsoft – $95,01. Общий дивидендный поток за год составляет 2,82/167,43*100=1,68% на одну акцию Apple и 1,72/95,01*100=1,81% на одну акцию Microsoft. Здесь приблизительный паритет.
5. БЕТА-НЕЙТРАЛЬНЫЙ ПОРТФЕЛЬ И ПАРНЫЙ ТРЕЙДИНГ
Кроме единицы, другим ключевым значением Бета для портфеля является ноль. Портфель, для которого Бета=0, называется бета-нейтральным или рыночно-нейтральным. Нейтральность портфеля ценных бумаг или иных финансовых инструментов лежит в основе стратегии парного трейдинга.
Чем хорош портфель с Бета=1 или около 1?
Он исключает собственный риск. СКО доходности портфеля равно или почти равно СКО доходности фондового индекса. В смысле доходности, такой портфель движется вместе с индексом. Его доходность растет на росте доходности индекса, но, увы, падает при уменьшении доходности индекса.
Обнуление Бета приводит к тому, что доходность портфеля не реагирует на изменение доходности рынка и зависит только от соотношения между входящими в него акциями.
Как привести суммарный Бета портфеля к нулю?
Первый, наиболее понятный путь – ввести в него бумаги с положительными и отрицательными Бета. Рассчитав (подобрав) необходимые веса, можно свети Бета в ноль. Способ сколь понятный, столь и почти неосуществимый в реальной жизни. Найти акцию, которая бы устойчиво падала при росте индекса дело непростое. Да и насколько надежен подобный инструмент для длинных позиций?
Гораздо проще поступить иначе. Сформировать портфель из длинных и коротких позиций. Тогда для длинных позиций Бета будут традиционно положительными. Для коротких – отрицательными, по модулю равными положительным Бета, если бы такие бумаги приобретались.
Проиллюстрируем сказанное на примере котировок акций, приведенных в предыдущем разделе.
Если половину портфеля составить из длинной позиции по акциям Microsoft с Бета=1,035, а вторую половину – из короткой позиции по акциям Apple с Бета=0,802, то итоговый Бета портфеля будет равен: 0,5*1,035+0,5*(-1)*0,802=0,116. Достаточно близко к нулю. Если бы инвестор поменял бы направления позиций местами, то есть, открыл бы по половине портфеля лонги в Apple, а по другой половине шорты в Microsoft, то и Бета портфеля изменил бы знак на противоположный и стал бы =-0,116.
В наборе из двух акций очень просто вычислить веса так, чтобы Бета точно был нулевым. Достаточно решить систему двух уравнений с двумя неизвестными:
В нашем случае (Microsoft в лонг, Apple в шорт), решая систему, имеем X(Microsoft)= 0,4366, X(Apple)=0,5634.
Проверка: 0,4366*1,035-0,5634*0,802=0,000342. То есть, с учетом округлений весов и Бет до тысячных – «крепкий» ноль.
Как заработать на бета-нейтральном портфеле?
Подробно об этом написано в статьях категории «Парный трейдинг» нашего сайта. Необходимо выбрать пару акций или иных активов с высокой степенью корреляции (с коэффициентом корреляции близким к 1) и оперировать спредом. Открывать длинные позиции по недооцененной акции и короткие по переоцененной на широком спреде и закрывать их на узком спреде.
Особенно любят такие стратегии хедж-фонды.
В заключение необходимо отметить, что Бета-коэффициент отдельной бумаги или портфеля – величина непрерывно изменяющаяся и подлежит пересчету при переходе от одного таймфрейма к другому. Кроме того, она зависит от размера выборки котировок.
Владимир Наливайский
ПРИМЕЧАНИЯ И ССЫЛКИ
- «Бета-нейтральный портфель», Википедия
- «Шарп, Уильям», Википедия.
- https://finviz.com
- https://finance.yahoo.com
- «Cреднеквадратическое отклонение», Википедия
ИСПОЛЬЗУЕМЫЕ СОКРАЩЕНИЯ
ЦБ – ценная бумага, по тексту под ЦБ понимается акция СКО – среднеквадратичное (среднеквадратическое, стандартное) отклонение, σ
Данные для построения коэффициента бета информационными компаниями
Коэффициент бета используется многими информационно-инвестиционными компаниями для оценки систематического риска: Bloomberg, Barra, Value Line и др . Для построения коэффициента бета используются месячные/недельные данные за несколько лет. В таблице показаны основные параметры оценки показателя различными информационными компаниями.
★ Инвестиционная оценка в Excel. Расчет NPV, IRR, DPP, PI за 5 минут
| Информационные компании | Исторический период наблюдения | Частота |
| Bloomberg | 2 года | Неделя |
| Barra | 5 лет | Месяц |
| Value Line | 5 лет | Месяц |
Можно заметить, что Bloomberg проводит краткосрочную оценку показателя, тогда как Barra и Value Line используют месячные данные доходностей акций и рынка за последние пять лет. Долгосрочная оценка может сильно быть искажена вследствие влияния на акции компании различных кризисов и негативных факторов.
Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс
Где смотреть коэффициент Альфа
Расчет всех исходных показателей для формулы вычисления альфы потребует много статистических данных за несколько лет. Мы такой задачи ставить не будем. Для рядового инвестора достаточно готовых и уже опубликованных значений коэффициента α. Данные можно найти в интернете на специализированных сервисах для поиска и сравнения фондов. Например, на pif.investfunds.ru, где можно сравнивать фонды сразу по нескольким коэффициентам, в том числе по α относительно индекса Мосбиржи. Для просмотра искомых показателей достаточно бесплатной регистрации.
Для удобства скачиваем таблицу ПИФов в Excel и фильтруем по альфе. Получаем 43 фонда с положительным коэффициентом α из 248 доступных позиций. Отрицательные величины у 205 ПИФов в списке, причем их значение достигает минус 7,31. Нельзя сказать, что это приговор для фондов внизу списка. Возможно, через пару лет они покажут положительный результат и сменят лидеров в ТОПе. Но на момент анализа, статистика предыдущих 3 лет говорит либо о неудачных инвестиционных решениях, либо о том, что плата за управление «съедает» прибыль инвестора.
На глобальном рынке, где господствуют взаимные фонды, гораздо шире представлены ресурсы по раскрытию альфы и беты mutual funds. Источниками данных могут быть, например, скринеры фондов от Wall Street Journal или Bloomberg. Здесь ситуация с альфой лучше, чем в России: не менее ¼ положительных результатов управления из более чем 40 тысяч фондов. Однако паи взаимных фондов в России доступны в ограниченном режиме только квалифицированным инвесторам и обладателям брокерского счета у зарубежного брокера.
Коэффициент бета в модели оценки капитальных активов – CAPM
Формула расчета доходности акций по модели капитальных активов CAPM (Capital Assets Price Model, модель У.Шарпа) имеет следующий вид:
где:
r – будущая ожидаемая доходность акций компании;
rf – доходность по безрисковому активу;
rm – доходность рынка;
β – коэффициент бета (мера рыночного риска), отражает чувствительность изменения стоимости акций компании в зависимости от изменения доходности рынка (индекса);
Модель CAPM была создана У.Шарпом (1964) и Дж. Линтером (1965) и позволяет спрогнозировать будущее значение доходности акции (актива) на основании линейной регрессии. Модель отражает линейную взаимосвязь планируемой доходности с уровнем рыночного риска, выраженного коэффициентом бета.
Доходность по безрисковому активу, на практике, берется как доходность по государственным ценным бумагам ГКО, ОФЗ. Доходность по ним в России составляет около 12%. Доходность можно посмотреть на сайте ЦБ в разделе «Ставки рынка ГКО-ОФЗ».
Для расчета рыночной доходности используют доходность индекса или фьючерса на индекс (индекс ММВБ, РТС – для России, S&P500 – США).
Формула расчёта
Формула для расчёта коэффициента β выглядит следующим образом:
Как видите без базовых знаний в области высшей математики здесь разобраться довольно трудно. Поэтому объясняю на пальцах. Суть расчёта сводится к тому, чтобы сопоставить динамику изменения курсовой стоимости конкретных акций с динамикой рынка акций в целом.
Если волатильность рассматриваемых бумаг превышает волатильность по рынку в целом, то это говорит о том, что они более чувствительны к изменению конъюнктуры. Это, в свою очередь, говорит нам о том, что инвестиции в них подвержены большему риску.
При этом нет нужды охватывать весь рынок целиком и забивать в формулу значения для каждой акции его составляющей. В данном случае достаточно использовать значение фондового индекса (который сам по себе представляет среднее значение курсовой стоимости акций принадлежащих к определённой отрасли или объединённых по какому-либо другому признаку).
Для акций российских эмитентов в данном случае можно применять индекс Мосбиржи, а для бумаг фондового рынка США, например, будет актуален индекс S&P500.
Индексы Мосбиржи и S&P500
Коэффициент Бета может быть рассчитан как для отдельных акций, так и для портфеля инвестора в целом. Бета коэффициент портфеля вычисляется как средняя величина Бета коэффициентов акций в него входящих (с учетом их весов).
Как же рассчитать данный коэффициент человеку не отягощённому знаниями в области высшей математике? Спешу вас успокоить, перефразируя высказывание одного из героев бессмертной комедии Гайдая, скажу: “Всё уже посчитано до нас!”
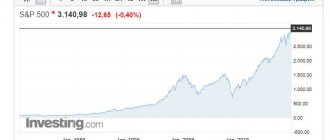
Вы легко можете найти данные по этому коэффициенту на множестве сайтов посвящённым тематике инвестиций и биржевой торговли. Вот например картинка с графиком и основными показателями акций ОАО Новатэк, взятая с сайта investing.com:
Пример расчета коэффициента бета в Excel
Рассчитаем коэффициент бета в Excel для отечественной . Данная компания имеет обыкновенные акции, котировки которых можно посмотреть на сайте finam.ru в разделе «Экспорт данных». Для расчета были взяты месячные котировки акции ОАО «Газпром» (GAZP) и индекса РТС (RTSI) за период с 31.01.2014 по 31.01.2015 г.
Далее необходимо рассчитать доходности по акции и индексу, для этого воспользуемся формулами:
D6=LN(B6/B5)
E6=LN(C6/C5)
Для расчета коэффициента бета необходимо рассчитать коэффициент линейной регрессии между доходностью акций ОАО «Газпром» и индекса РТС. Рассмотрим два варианта расчета коэффициента бета средствами Excel.
Вариант №1. Расчет через формулу Excel
Расчет через формулы Excel выглядит следующим образом:
=ИНДЕКС(ЛИНЕЙН(D6:D17;E6:E17);1)
Вариант №2. Расчет через надстройку «Анализ данных»
Второй вариант расчета коэффициента бета использует надстройку Excel «Анализ данных». Для этого необходимо перейти в главном меню программы в раздел «Данные», выбрать опцию «Анализ данных» (если данная надстройка включена) и в инструментах анализа выделить «Регрессия». В поле «Входной интервал Y» выбрать доходности акции ОАО «Газпром», а в поле «Выходные интервал X» выбрать доходности индекса РТС.
Далее мы получим отчет по регрессии на отдельном листе. В ячейке В18 показано значение коэффициента линейной регрессии, который равен коэффициенту бета = 0,46. Также проанализируем другие параметры модели, так показатель R-квадрат (коэффициент детерминированности) показывает силу взаимосвязи между доходностью акции ОАО «Газпром» и индекса РТС. Коэффициент детерминированности равен 0,4, что является довольно мало для точного прогнозирования будущей доходности по модели CAPM. Множественный R – коэффициент корреляции (0,6), который показывает наличие зависимости между акцией и рынком.
Значение 0,46 коэффициента бета для акции свидетельствует о умеренном риске и в тоже время сонаправленность изменения доходностей.
| ★ Программа InvestRatio – расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса |
Плюсы и минусы коэффициента Альфа
К преимуществам использования коэффициента Альфа следует отнести следующее:
- Расчет альфы строится на обширных статистических данных за несколько лет. Это делает его значение основанным на больших объемах реальных результатов. Конечно, это не исключает элемента случайности, но сводит его к минимуму. Сам Дженсен в своих исследованиях закладывал 4—6% допущения.
- Инвестор получает в готовом виде числовое измерение качества управления. На основании показателя он может судить о квалификации и профессиональной интуиции управляющего.
- Альфа учитывает не только доходность, но и меру риска в виде заложенной в формулу беты. Тем самым из двух фондов с равной доходностью он может выбрать тот, у которого лучший показатель альфы.
Рекомендую прочитать также:
Убытки БКС: стоит ли беспокоиться инвесторам
У компании БКС серьезные проблемы с убытками
В том, что составляет преимущества альфы, отчасти заложены и его недостатки, в том числе обусловленные российской спецификой.
- Необходимость сбора больших статистических данных делают его расчет уделом узкого круга профессионалов. Для рядового инвестора слишком трудозатратно самостоятельно перепроверять значение α.
- Положительная альфа по результатам управления в прошлом вовсе не влечет за собой такой же эффективности в будущем. Мерилом успешности мог бы быть достаточно длительный период наблюдений, как это было у Майкла Дженсона. Однако на молодом российском рынке за 10–15 лет происходит столько изменений, что ценность расчетов коэффициента на таком горизонте становится ничтожной.
- Уже в самой формуле альфы изначально зашита неопределенность в виде коэффициента бета (мера риска). А он, как мы знаем, меняется во времени, особенно на волатильных рынках вроде российского.
Недостатки использования коэффициента бета в модели CAPM
Рассмотрим ряд недостатков присущих данному коэффициенту:
- Сложность использования коэффициента бета для оценки низколиквидных акций. Данная ситуация характерна для развивающихся рынков капитала, в частности: России, Индии, Бразилии и т.д.
- Не возможность оценки малых компаний, не имеющих эмиссий обыкновенных акций. Большинство отечественных компаний не проходили процедуры IPO.
- Неустойчивость прогноза коэффициента бета. Использование линейной регрессии для оценки рыночного риска по ретроспективным данным не позволяет получать точные прогнозы риска. Как правило, трудно прогнозировать коэффициент бета более 1 года.
- Не возможность учета несистематических рисков компании: рыночной капитализации, исторической доходности, отраслевой принадлежности, критериев P/E и т.д., которые оказывает влияние на величину ожидаемой доходности.
Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс
Стоит ли использовать коэффициенты
Безусловно, каждый сам определяет, стоит ли ориентироваться на значения коэффициентов при выборе фонда. На наш взгляд, использовать коэффициенты можно, но лишь как вспомогательную информацию. При этом необходимо использовать ее по коэффициентам в совокупности, а не опираться только на один из них. И, конечно же, значения коэффициентов должны быть рассчитаны относительно корректного эталона (индекса).
Окончательным критерием, по которому следует определять эффективные управляющие компании и фонды, является наличие системы по управлению капиталом. Если у фонда высокий результат и хорошие показатели по коэффициентам, то необходимо разобраться в способах, которыми этот результат достигается. В случае если результаты зависят от одного единственного управляющего, вам предстоит внимательно следить за его карьерой, ведь только от него будет зависеть результативность ваших инвестиций. Если же в компании выстроена система по управлению капиталом, то в данном случае эффективность ваших инвестиций не будет зависеть от одного человека. Напротив, человеческий фактор здесь уже сведен к минимуму, а сама система является интеллектуальной собственностью компании.
Модификация коэффициента бета
Так как коэффициент, предложенный У. Шарпов не имел должной устойчивости и не мог использоваться для прогнозирования будущей доходности в модели CAPM, различными учеными были предложены модификации и корректировки данного показателя (англ. adjusted beta, modified beta).Рассмотрим скорректированные коэффициенты бета:
Модификация коэффициента бета от М.Блюма (1971)
Маршал Блюм показал, что со временем коэффициенты бета компаний стремятся к 1. Формула расчета скорректированного показателя следующая:
Использование данных весовых значений позволяет более точно спрогнозировать будущий систематический риск. Так данную модификацию используют многие информационные агентства, такие как: Bloomberg, Value Line и Merrill Lynch.
Модификация коэффициента бета от Бава-Линдсберга (1977)
В своей корректировке Линдсберг предложил рассчитывать односторонний коэффициент бета. Главный постулат заключался в том, что изменение доходности выше определенного уровня большинство инвесторов не рассматривают как риск, а риском считается только то, что ниже уровня. За минимальный уровень риска в данной модели был доходность безрискового актива.
где:
ri – доходность акции; rm – доходность рынка; rf – доходность безрискового актива.
Модификация коэффициента бета от Шоулза-Виллимса
β-1, β, β1 – коэффициенты беты для предыдущего (-1) текущего и следующего (1) периода;
ρm – коэффициент автокорреляции рыночной доходности.
Модификация коэффициента бета от Харлоу-Рао (1989)
Формула отражает одностороннюю бету, с предположением, что инвесторы рассматривают риск только как отклонение от среднерыночной доходности вниз. В отличие от модели Бава-Линдсберга за минимальный уровень риска брался уровень среднерыночной доходности.
где: μi – средняя доходность акции; μm – средняя доходность рынка;
Помимо коэффициента бета на практике используют другие показатели риска-доходности инвестиционного портфеля, ПИФа, более подробно узнать про современные показатели оценки инвестиций вы можете в моей статье: “Оценка эффективности инвестиций, инвестиционного портфеля, акций на примере в Excel“. О практике оценке риска инвестиции читайте в статье: “Методы оценки риска VaR (Value at Risk). Рыночный риск. Пример расчета в Excel “.
Для чего применяют бету
На практике бету применяют в двух случаях.
Первый – это прогнозирования движения акции в будущем. Если у акции бета равна 1,5, то логично предположить, что при росте рынка на 10% она подорожает на 15%. Причем, чем больший отрезок времени взят, тем точнее будет прогноз.
Минус этого подхода заключается в том, что бета показывает прошлую взаимосвязь актива и рынка. И если рыночная ситуация изменилась (или изменилась сама акция), то прогнозирование будет, мягко говоря, неточным. По прошлым результатам нельзя точно предсказать поведение акции, можно только предположить.
Поэтому корректнее говорить так: если у акции бета равна 1,5, то в будущем, скорее всего, она подорожает на 15%, если рынок за этот период вырастет на 10.
Не забывайте об этом моменте.
И второй случай практического применения беты – это оценка успешности управления фондом. Анализируя альфу и бету, можно понять, где управляющий проявил себя профессиональнее, а где фонду дал вырасти рынок – и особой заслуги управляющего в этом не было.
Коэффициент бета для акций США
Существуют сервисы позволяющие оценить коэффициент бета для множества компаний и выделить наиболее интересные. Будем применять сервис Finviz. Чтобы найти акции менее чувствительные чем колебания фондового рынка необходимо установить коэффициент бета меньше 1.
Фильтрация акций США по бета меньше “1” позволяет найти акции для консервативного инвестора, изменчивость которых ниже изменения индекса S&P 500
Как понимать бету
Ок, нашли бету. Как интерпретировать ее?
Если бета больше 1. Это значит, что акция колеблется значительно сильнее рынка. Например, если бета равна 2, то при росте рынка на 10% акция вырастет на 20%. И, аналогично, при падении рынка на 10% акция упадет на 20%. На рынке США есть такой термин, как high-beta stock. Это наиболее волатильные акции, которые привлекают массу спекулянтов, так как на широком движении можно хорошо заработать. Долгосрочным инвесторам лучше избегать акций с излишне высокой бетой.
А вот еще интересная статья: Как покупать акции, используя коэффициент Грэма
Если бета равна 1 или около того. Это значит, что волатильность рынка и ценной бумаги находится примерно на одном уровне. И если рынок будет расти на 5%, то акция тоже вырастет примерно на 5%. Консервативному инвестору, желающему зарабатывать примерно на уровне рынка, следует отбирать акции именно с такой бетой.
Если бета меньше 1, но больше 0. Это значит, что акция менее волатильна, чем рынок. Например, при бете в 0,5 при росте рынка на 20% акция подорожает только на 10%. С другой стороны, если рынок упадет на 20%, то акция потеряет в цене только 10%. Включая такие акции в портфель, вы ограничивает потенциальную доходность, но одновременно снижаете риски.
Если бета равна 0. Это значит, что акция вообще не коррелирует с рынком. Такое бывает, но редко. Чаще всего нулевая бета у стартапов и, напротив, хорошо развитых компаний, которые растут не угроз со стороны внешних факторов. Пример – акции телекомов и ритейлеров.
Если бета меньше 0. Это значит, что акция движется в противофазе рынку. Например, акции золотодобывающих компаний традиционно растут, когда рынок падает, так как золото считается защитным активом и инвесторы перекладываются в него при непонятных ситуациях. С помощью акций с отрицательной бетой можно захеджировать свои риски. При росте рынка такие акции будут падать, но при падении – напротив, вырастут.
Выводы и рекомендации
- Рассмотренные коэффициенты обладают рядом недостатков, а потому не в полной мере позволяют оценить эффективность результатов, которые демонстрирует управляющий.
- При выборе управляющей компании и фонда можно использовать коэффициенты как вспомогательную информацию. Принимая окончательное решение, нужно ориентироваться на систему (способы) по управлению капиталом, которая используется в той или иной компании.
- Стоит помнить о том, что основная задача управляющей компании заключается в формировании эффективной системы управления капиталом. Высокое качество управления капиталом и значения коэффициентов будут являться следствием выполнения этой задачи.